1. Gradient Descent with Large Datasets
최근 머신러닝 알고리즘이 더 높은 성능을 보이는 이유 중 하나는 훈련할 수 있는 데이터의 양이 엄청나게 많아졌기 때문이다. 이런 대규모 데이터가 있을 때 처리하는 방법에 대해 알아볼 것이다.
[Learning With Large Datasets]
이전에도 잠깐 봤었지만,

머신러닝에서 알고리즘이 중요한 게 아니라 데이터의 양이 성능에 중요한 영향을 끼친다.
하지만 이렇게 데이터가 많을 때는 계산적인 문제(Computational problems)가 발생하게 된다.
예를 들어 100,000,000 개의 샘플을 가지고 있다고 생각해보자.

그러면 Gradient Descent를 한 단계 진행하기 위해서 100,000,000번의 덧셈을 해야 한다. 따라서 다른 효율적인 방법이 필요하다.
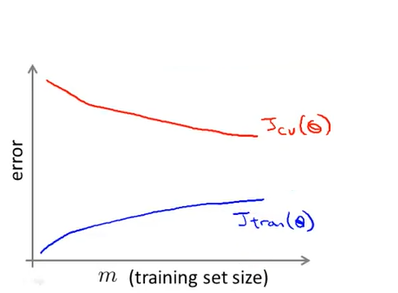
예를 들어 랜덤 하게 1,000개의 데이터만 뽑아서 학습을 시켰을 때 다음과 같이 Learning Curve를 그려볼 수 있다.

만약, 위와 같이 \(J_{cv}(\theta)\)와 \(J_{train}(\theta)\)이 수렴한다면, 100,000,000개의 데이터를 모두 학습할 필요가 없을 것이다.
반대로, 아래와 같이 High Variance 형태로 그래프가 그려진 경우에는 데이터를 더 많이 사용하면 성능이 올라갈 것이다.
이제 대규모 데이터 셋을 다루기 위한 효율적인 방법 두 가지, Stochastic Gradient Descent와 Map Reduce에 대해 알아볼 것이다.
[Stochastic Gradient Descent]
우리는 그동안 Gradient Descent를 사용해서 비용 함수를 최소화했었다. 이때, 많은 양의 데이터를 다룬다면 Gradient Descent의 연산 비용은 매우 커질 것이다.
Linear Regression 모델에 대해 Gradient Descent를 적용하는 것을 다시 기억해보자. 우리의 가설 함수와 비용 함수의 식, Gradient Descent 알고리즘, 그리고 \(\theta_0, \, \theta_1\)에 대한 비용 함수의 그래프는 다음과 같다.
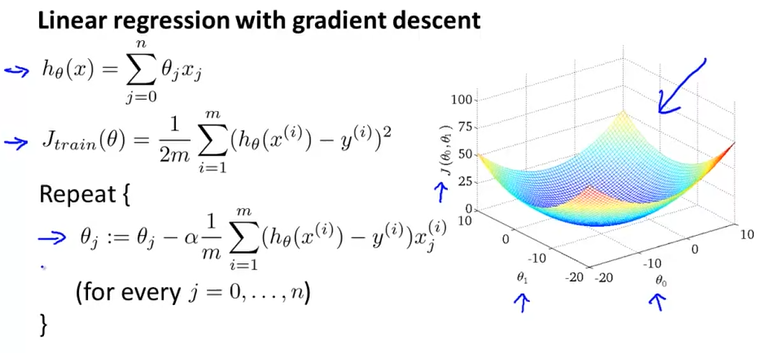
이것을 2차원을 나타내면 다음과 같은데,

Gradient Descent 알고리즘을 반복 진행함에 따라 위와 같이 점점 global minimum으로 수렴해 갈 것이다.
이렇게 모든 샘플 m에 대해서 경사 하강법을 진행하는 것을 Batch Gradient Descent라고 부른다. 그런데 데이터가 매우 많은 경우(예를 들어 300,000,000개) Batch Gradient Descent를 사용하면, 연산량이 매우 많아져서 여러 문제가 발생한다.
따라서 Large Dataset을 다루기 위해 새로운 방법이 등장했는데, 바로 Stochastic Gradient Descent이다.

Stochastic Gradient Descent의 비용 함수는 모든 m에 대한 것이 아니라, i번째 샘플의 cost만을 뜻한다. 따라서 모든 m개의 샘플의 cost를 더하는 것이 아니라, 한 개의 샘플의 cost만을 비용 함수로 사용한다. 그러면 미분도 i번째 샘플에 대해서만 계산하면 되므로 연산이 간단해진다.
Stochastic Gradient Descent의 진행 방법은 다음과 같다.

- 랜덤하게 데이터 셋을 섞는다.
- Gradient Descent를 하나의 샘플에 대해서만 반복한다. (즉, 한 iteration 당 하나의 샘플만을 사용)
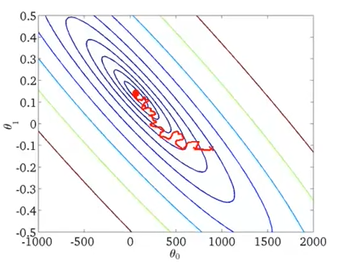
SGD(Stochastic Gradient Descent)를 사용하면 다음 그래프의 분홍색 선과 같이 랜덤 하게 최적점을 찾아나간다. (빨간색 선은 GD)

반복 한번 당 하나의 랜덤 샘플만을 이용하기 때문에, GD에 비해 정확하게 최적점을 찾지는 못하고 최적점 근처에서 왔다 갔다 하며 수렴하게 된다. 따라서 성능은 조금 떨어지지만 속도는 확실히 빨라지는 장점을 갖고 있다.
[Mini-Batch Gradient Descent]
Mini-Batch Gradient Descent는 앞의 두 방법의 중간이라고 보면 된다.

b를 mini-batch size라고 하면, 각 iteration마다 b개의 샘플을 사용해서 Gradient Descent를 진행한다. b는 보통 2개 ~ 100개 정도로 선택한다.
예를 들어, b = 10, m = 1000으로 가정하고 알고리즘을 살펴보면 다음과 같다.

샘플을 10개 뽑은 다음, i부터 i+9 샘플에 대해서만 미분항을 구하고 최적화를 진행한다.
Mini-batch Gradient Descent는 Vectorization이 잘 되어있을 때 Stochastic Gradient Descent에 비해 outperform 한 성능을 보여준다. Mini-batch의 크기 b를 조절하면서 시간이 걸릴 수는 있지만, Stochastic Gradient Descent보다 더 빠르게 구현될 수도 있다.
[Stochastic Gradient Descent Convergence]
Gradient Descent에서 알고리즘이 수렴하고 있는지 확인하는 것 또한 중요하다. 마찬가지로, Learning Rate인 \(\alpha\)를 조절하는 것도 중요하다.

이전까지 Batch Gradient Descent를 할 때는, \(J_{train}(\theta)\) 그래프를 매 iteration마다 그려서 수렴을 확인했었다.

Stochastic Gradient Descent를 할 때는, cost를 저장해놨다가 1000번의 iteration마다 그 평균을 구해서 plot 하고 그래프는 다음과 같다.

파란색 선을 보면 노이즈가 생기며 그래프가 그려지고, 매 iteration마다 감소하지 않을 수도 있다. 빨간색 선은 Learning rate를 작게 설정한 그래프다. 조금 더 늦게 감소하고 있지만, 결국에는 파란 그래프보다 저 적은 값으로 수렴한다. 따라서 Learning rate가 작을 때 더 좋은 parameter 값을 얻는 경우도 있다.
이번에는 파란 선은 1000 iteration마다, 빨간 선은 5000 iteration마다 그래프를 그린 것이다.

5000 iteration마다 그린 그래프가 좀 더 노이즈가 적은 곡선에 가까운 모습을 보인다.
가끔은 이렇게 cost가 감소하지 않는 것 같은 그래프가 그려질 때도 있다.

이럴 때는 iteration을 1000 -> 5000과 같이 늘려주면 빨간색 선이나 보라색 선처럼 경향을 파악할 수 있게 된다. 만약 보라색 선처럼 평평한 그래프를 그린다면, 학습 알고리즘이 제대로 작동하지 않다는 뜻이므로 Learning Rate나 feature 등을 변경해봐야 한다.
마지막으로, 아래와 같이 오히려 cost가 발산하는 그래프가 나올 수 있다.

이런 경우에는 Learning Rate를 더 작게 설정해야 한다.
정리하면, 그래프의 노이즈가 너무 심하거나 진동 때문에 경향성 파악이 힘들다면 iteration을 늘려주고, cost가 발산하면 Learning rate를 작게 설정해주면 좋다.
마지막으로 Learning rate에 대해 조금 더 알아보자.

일반적으로 Stochastic Gradient Descent를 사용하면 오른쪽 그래프와 같이 랜덤 하게 움직이며 최적점 근처를 맴돌게 된다. 따라서 정확한 최적 값을 얻기는 힘든데, 이를 개선하기 위해서 Learning rate를 천천히 감소시키는 방법이 있다. 아래와 같이 \(\alpha\)를 설정하는데, const1과 const2는 추가적인 매개변수이다.
$$ \alpha=\frac{const1}{iterationNumber+const2} $$
이 방법을 잘 사용하면 다음과 같이 Batch Gradient Descent와 비슷하게 최적점을 찾아나간다.
하지만 사람들이 잘 사용하지 않는데, 그 이유는 추가적인 매개변수 const1과 const2를 다루어야 하고 알고리즘이 복잡해질 수 있기 때문이다.
2. Advanced Topics
[Online Learning]
지금까지는 이미 수집된 데이터를 이용해서 학습을 진행했다. Online Learning setting을 이용하면 계속해서 데이터가 수집되는 상황에서 모델링이 가능하다. 많은 대형 웹사이트에서 다양한 online learning algorithm을 통해 유저 정보를 지속적으로 학습하고 있다.
예를 들어, 출발지와 도착지를 입력하면 견적을 내주는 운송 서비스 웹사이트가 있다고 생각해보자. 유저들은 이 사이트에서 서비스를 이용할 수도 있고(y=1) 아닐 수도 있다(y=2). Feature \(x\)는 사용자 정보, 출발지/도착지, 견적 가격 등이 될 수 있고, 가격 최적화를 위해 \(p(y=1\mid x;\theta)\)를 학습시키려 한다.

우리가 웹사이트를 계속 동작시킨다면, 하나의 Online Learning 알고리즘이 계속 실행될 것이다. 이 알고리즘은 parameter \(\theta\)를 계속 업데이트하는데, 고정된 training set을 사용하는 게 아니라, 유저에게 얻은 새로운 (\(x,y\))를 통해 학습하고 버린다.

Online Learning 알고리즘은 계속해서 유저가 유입되는 웹사이트 같은 곳에서 사용하기 유리하다. 데이터가 아주 많고, 계속해서 수집된다면, 이미 학습한 샘플을 다시 볼 필요가 없다. (만약 사용자가 적다면 online learning보다는 고정된 training set을 통해 학습하는 것이 더 좋다.) 이 방법을 사용하면 변화하는 유저의 성향에 적응할 수 있다.
다른 예시로, 유저에게 적절한 검색 목록을 제공하는 online learning 알고리즘이 있다.

가게에 100대의 휴대폰이 있다고 생각해보자. 여기서 유저가 "Android phone 1080p camera"라고 검색을 했을 때, 10대의 휴대폰 목록을 보여주려고 한다.
이를 해결하기 위해서는 각 휴대폰에 대해서 유저 쿼리가 제공되고, feature vector \(x\)로는 휴대폰의 feature, 유저 쿼리와 휴대폰의 이름/설명이 얼마나 많이 일치하는지 등을 사용한다. 그리고 유저가 클릭할 확률이 가장 높은 10개의 휴대폰을 리스트업 한다.

이런 문제를 Click-Through Rate(CTR);클릭률 문제라고 하는데, 유저가 특정 링크를 클릭할 확률을 학습하는 것이다.
[Map Reduce and Data Parallelism]
이전까지는 하나의 장치나 컴퓨터에서 실행할 수 있는 경우였다. 하지만 데이터가 너무나 방대해서 하나의 컴퓨터로는 실행할 수 없는 경우는 어떻게 해야 할까?
Map Reduce approach라고 불리는 Large-scale에 대한 다른 접근법을 알아보자.
우리가 Linear regression이나 Logistic regression 모델을 학습하려고 하고, batch-gradient descent를 사용한다고 생각해보자. (m=400)
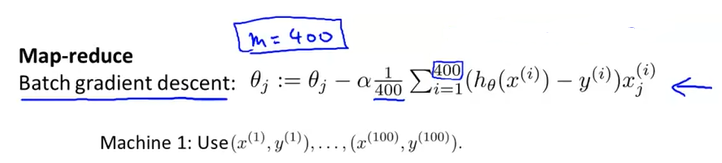
Map reduce의 아이디어는 다음과 같다.

- 400개의 샘플을 나누는데, 만약 4대의 컴퓨터를 사용한다면 4개의 subset으로 나누어서 각 컴퓨터마다 100개의 샘플을 학습하게 한다.
- 이렇게 구해진 각각의 \(temp_j\)들을 master 서버로 보낸 다음, 합쳐서 \(\theta_j\)를 업데이트한다.
Map-reduce에 대한 일반화 이미지는 다음과 같다.

Training set을 나눈 다음 각 컴퓨터로 보낸 뒤, 합쳐서 결과를 만들어낸다.
많은 학습 알고리즘이 training set에 대한 함수의 합으로 표현될 수 있기 때문에, 대용량의 데이터를 가지고 학습할 경우 Map-reduce 방법을 사용해서 병렬적으로 처리하면 연산 비용 문제를 해결할 수 있다.
Map-reduce는 하나의 컴퓨터를 이용해서도 가능한데, multi-core를 이용한 방법이다.

이전에 본 것과 마찬가지로, 각 코어마다 병렬적으로 계산을 수행한 뒤 합쳐서 결과를 낸다. 이 방법을 사용하면, 여러 컴퓨터로 Map-reduce를 사용했을 때, data center에서 정보를 받아올 때 생기는 네트워크 지연 문제를 방지할 수 있다.
이번 강의에는 Large scale dataset에서의 machine learning에 대해 알아봤다.
다음 강의는 응용 예제로, Photo OCR에 대한 것인데 따로 정리하지는 않을 것이다.
이상으로 앤드류 응 교수님의 머신러닝 강의 정리를 마친다.
* 공부 정리 목적으로 쓴 글입니다. 오타나 수정사항이 있으면 바로 알려주세요.
'데이터 사이언스 공부노트 > 머신러닝, 딥러닝' 카테고리의 다른 글
| [코세라 강의 정리] 앤드류 응의 머신러닝 - Recommender Systems (0) | 2021.09.04 |
|---|---|
| [코세라 강의 정리] 앤드류 응의 머신러닝 - Anomaly Detection (0) | 2021.09.03 |
| [코세라 강의 정리] 앤드류 응의 머신러닝 - Dimensionality Reduction (PCA) (0) | 2021.08.30 |
| [코세라 강의 정리] 앤드류 응의 머신러닝 - Unsupervised Learning (Clustering) (0) | 2021.08.29 |
| [코세라 강의 정리] 앤드류 응의 머신러닝 - SVM : Kernels (0) | 2021.08.28 |



