
Neural Network에서 m개의 Training sample이 있을 때, 용어를 다음과 같이 정의한다.
- \(L\) = network의 총 layer 개수
- \(s_l\) = \(l\) 층의 유닛 개수(bias unit 제외)
- \(K\) = output layer에서 유닛 개수 (class 수)
위의 신경망 구조에서는 \(L=4\), \(s_2=5\), \(s_4=K=4\) 가 된다.
1. Cost Function
이제 신경망(Neural Network)에서의 비용 함수(cost function)와 Parameter(\(\theta\))를 구해줘야 한다.
Neural Network의 activation function(\(a\))인 logistic(sigmoid) function을 사용하는 Logistic regression에서 비용 함수를 다시 살펴보면 아래와 같다.

Neural network는 class의 개수만큼 output layer의 노드가 만들어지므로 가설 함수의 차원도 \(K\) 개만큼 늘어난다.

따라서, 비용 함수에 다음과 같이 class의 개수만큼 더 생기는 오차들을 더해주고 regularization 항도 각 층마다 더해주면 되는데, 일반화된 식은 다음과 같다.

$$ J(\Theta) = -\frac{1}{m}\left
[\sum_{i=1}^{m}{\color{Red}\sum_{k=1}^{K}}y_{{\color{Red}k}}^{(i)}log(h_{\Theta}(x^{(i)}))_{{\color{Red}k}} + (1-y_{{\color{Red}k}}^{(i)})log(1-(h_{\Theta}(x^{(i)}))_{{\color{Red}k}})
\right ]
+ \frac{\lambda}{2m}{\color{Blue}\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}}\sum_{j=1}^{{\color{Blue}s_{l+1}}}{\color{Blue}(\Theta_{ji}^{(l)})^2} $$
- 빨간색으로 추가된 부분은 output 노드가 여러개(\(K\)개)이기 때문에 \(error\)도 \(K\) 개만큼 나오고, 그것들을 모두 더해주는 항이다.
- 파란색으로 추가된 부분은 Regularization(규제, 정규화)항인데, 'bias unit'은 규제 대상이 아니므로 \(\Theta_{j,i}\)의 차원은 (\(s_{j+1}\) x (\(s_{j}\))이 된다. 따라서 각 층마다 다음과 같은 가중치 행렬이 만들어지고, 그것들을 계산하여 더한 항이다.
$$\Theta^{(l)} =
\begin{bmatrix}
\Theta^{(l)}_{1,1} & \Theta^{(l)}_{1,2} & ... & \Theta^{(l)}_{1,s_l} \\
\Theta^{(l)}_{2,1} & \Theta^{(l)}_{2,2} & ... & \Theta^{(l)}_{2,s_l} \\
... & ... & ... & ... \\
\Theta^{(l)}_{s_{l+1},1} & \Theta^{(l)}_{s_{l+1},2} & ... & \Theta^{(l)}_{s_{l+1},s_l}
\end{bmatrix}$$
2. Backpropagation Algorithm
Cost function을 최소화하는 \(\Theta\)를 구하기 위해서는 두 가지가 필요한데, cost function인 \(J(\Theta)\)는 위에서 정의했으므로 편미분 \(\frac{\partial}{\partial \Theta^{(l)}_{i,j}}J(\Theta)\)를 계산해줘야 한다.
일반적인 식과 달리 Neural Network에서는 많은 층을 거쳐서 출력 값에 도달했기 때문에 미분을 하려면 연산량이 엄청 많아진다. 따라서 뒤에서부터 계산해주는 Backpropagation(역전파) 알고리즘을 사용하면 효율적으로 미분 계산이 가능해진다.
하나의 샘플을 가진 다음과 같은 신경망을 예로 들어보자.

우선, 출력 값을 구해야 하기 때문에 지난 시간에 배웠던 순전파를 사용해서 계산을 진행한다.
그다음 \(error\)를 계산하기 위해서 역전파를 사용하는데, 순전파와는 반대로 output layer에서부터 시작해서 최종 결과의 \(error\)를 먼저 구하고 이것을 이용해서 그 전 layer의 \(error\)를 계산하는 방식이다.
여기서 새로운 용어가 등장한다.
- \(\delta_j^{(l)}\)는 \(l\) 층의 노드 \(j\)에서의 \(error\)를 뜻한다.
예를 들어, output layer인 \(layer L=4\) 의 오차를 구하면 다음과 같이 간단하게 구할 수 있다.
$$ \delta_j^{(4)} = a_j^{(4)} - y_j $$
만약 벡터로 표현한다면
$$ \delta^{(4)} = a^{(4)} - y $$가 될 것이다.
이제 이전 layer의 \(\delta\)들을 구해야 하는데, 다음과 같은 공식을 사용한다.
$$\delta^{(3)} = (\Theta^{(3)})^{T}\delta^{(4)}.*g'(z^{(3)}))$$
$$\delta^{(2)} = (\Theta^{(2)})^{T}\delta^{(3)}.*g'(z^{(2)}))$$
- 여기서 '.*' 기호는 행렬곱 연산이 아니라 행렬의 element끼리의 곱을 의미한다.
\(g'()\)은 sigmoid function을 미분한 것이고 다음과 같다.
$$ g'(z^{(3)}) = a^{(3)}.*(1-a^{(3)}) $$
$$ g'(z^{(2)}) = a^{(2)}.*(1-a^{(2)}) $$
Input layer에 대해서는 변경하지 않을 것이므로 \(\delta^{(1)}\)은 구하지 않는다.
마지막으로 우리가 원하는 편미분 \(\frac{\partial}{\partial \Theta^{(l)}_{i,j}}J(\Theta)\)항을 구해줘야한다. 계산은 매우 복잡한데, Regularization 항을 제외하고 계산해주면 다음과 같다(나중에 추가시켜 줄 것임).
$$ \frac{\partial}{\partial \Theta^{(l)}_{i,j}}J(\Theta) = a_j^{(l)}\delta_j^{(l+1)} (\lambda = 0) $$
이해를 돕기 위해 역전파를 도식화하면 다음과 같다.


최종 결과의 오차를 단순하게 (output - expected)로 계산한다. 그다음 이전 layer로 추적해나가는 방식이다.
이제 하나의 샘플이 아닌, 여러 개의 샘플이 있는 데이터에서의 절차를 살펴보자.

- \(\Delta_{ij}^{(l)}\)는 우리가 구할 \(a_j^{(l)}\delta_j^{(l+1)}\)들을 누적해서 더한 값이다. 따라서 모든 \(l, i, j\)에 대해서 0으로 초기화시켜주는 작업을 해준다. 이것은 나중에 편미분 \(\frac{\partial}{\partial \Theta^{(l)}_{i,j}}J(\Theta)\)항을 계산할 때 사용된다.
- 그다음 모든 layer(L개)에 대해서 Forward propagation으로 \(a^{(l)}\)을 구해주고, backpropagation으로 \(\delta^{(L-1)}\)을 구해준다.
- 그리고 그 두 항을 곱해서 \(\Delta_{ij}^{(l)}\)에 누적하여 더한다.
- 이 과정들을 모든 샘플(m개)에 대해서 반복한다.
위 사진에서 \(\Delta_{ij}^{(l)}\)을 누적해서 더하는 식을 벡터화 표현한다면 다음과 같다.
$$ \Delta^{(l)} := \Delta^{(l)} + \delta^{(l+1)}(a^{(l)})^T $$
위의 과정을 모두 마치면, 최종적으로 다음과 같이 \(D\)를 계산해준다.

위의 식을 보면 두 가지 경우가 나오는데, \(j=0\) 인 경우는 "bias"항에 대응된다. 따라서 Regularization 항이 없는 것을 볼 수 있다.
증명은 복잡하지만, \(D\)항을 계산해보면 우리가 구하고자 한 cost function의 편미분이므로 우리는 이것을 가지고 gradient descent나 다른 고급 알고리즘에 사용할 수 있다.

3. Backpropagation Intuition
우선 Forward propagation의 진행 과정을 다시 한번 살펴보자.

위와 같이 hidden layer가 2개인 신경망이 있을 때, 각 층의 노드들은 이전 층의 노드들과 가중치의 계산으로 구해지고 출력 값은 계산한 값에 활성 함수를 씌운 값이다.
예를 들어 layer3의 첫 번째 노드를 계산하려면,
$$z_1^{(3)} = \Theta_{10}^{(2)}*1 + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)} $$
로 구할 수 있다. 그리고 출력 값(다음 노드의 입력값)은 \(z\)에 활성 함수를 적용시켜준 값이다.
역전파는 반대 방향인 오른쪽에서 왼쪽으로 계산해주면 된다.

출력층에서의 오차 \(\delta_1^{(4)}\) 값은 \(y^{(i)}-a_1^{(4)}\)로 구해진다.
그리고 은닉층에서의 \(\delta\)들은 미분을 통해서 계산해야 하는데, 예를 들어 \(\delta_2^{(2)}\)를 계산한다고 생각해보자.
노드 \(a_2^{(2)}\)는 \(\Theta^{(2)}_{12}\)와 계산되어 \(a_1^{(3)}\)에 영향을 줬고, \(\Theta^{(2)}_{22}\)와 계산되어 \(a_2^{(3)}\)에 영향을 줬다. 따라서 \(\delta_2^{(2)}\)는 다음과 같이 구할 수 있다.
$$ \delta_2^{(2)} = \Theta^{(2)}_{12}\delta^{(3)}_1 + \Theta^{(2)}_{22}\delta^{(3)}_2 $$
또, \(\delta_1^{(3)}\)는 다음과 같이 구할 수 있다
$$ \delta_1^{(3)} = \Theta^{(3)}_{11}\delta^{(4)}_1 $$
※ \(\delta_0^{(l)}\) 항은 "Bias unit"이므로 신경 쓰지 않는다.
[Backpropagation in Practice]
신경망을 실제로 적용할 때 적용하는 방법들을 소개한다.
우선, 학습을 위해서 어떤 구조의 신경망을 사용할 것인지 정한다.

- Input unit의 개수 : 특성 \(x\)의 차원
- Output unit의 개수 : Class의 수
- Hidden layer와 unit의 개수 : Hidden layer는 늘어날수록 성능이 좋지만 연산 속도도 늘어난다.
다음으로, Training a neural network의 과정이다.
- 가중치를 랜덤 하게 초기화시킨다. (모두 0으로 설정 X)
- 순전파를 통해 모든 \(x^{(i)}\)에 대해 \(h_\Theta(x^{(i)})\)를 구한다.
- Cost function \(J(\Theta)\)를 구한다.
- 역전파를 통해 \(\frac{\partial}{\partial\Theta_{jk}^{(l)}}J(\Theta)\)를 구한다.
- Gradient checking을 통해 역전파가 제대로 계산되는지 확인 후 해당 코드 disable 처리해준다.
- Gradient descent나 다른 최적화 방법을 통해서 \(J(\Theta)\)를 최소화하는 \(\Theta\)를 찾는다.
Neural network의 경우 cost function이 non-convex 하기 때문에 Local optima에 갇힐 수도 있다. 하지만 큰 문제는 아니고, 일반적으로 gradient descent나 다른 최적화 방법이 잘 동작하기 때문에 Global optima를 찾지 못하더라도 좋은 수준의 Local optima를 얻을 수 있다.
Gradient Descent 알고리즘의 3D plot을 다시 한번 상기시켜보자.
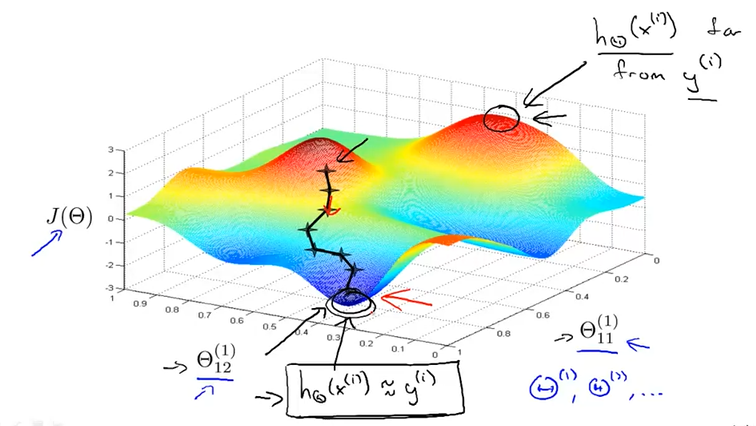
최고점(붉은색)의 위치에서 가설 함수는 실제값과 가장 큰 차이가 있고, 최저점(파란색)의 위치에서 실제값과 가장 유사하다. Gradient descent 알고리즘은 Random 한 위치에서 시작해서 경사를 따라가며 최저점을 찾는 역할을 한다. 이때, backpropagation은 어디로 갈지 방향을 설정해주는 역할을 한다.
이번 강의에서는 신경망에서 역전파 알고리즘에 대해 알아봤다.
다음 강의에서는 머신 러닝을 적용할 때 몇 가지 조언들에 대해 알아볼 것이다.
* 공부 정리 목적으로 쓴 글입니다. 오타나 수정사항이 있으면 바로 알려주세요.
'데이터 사이언스 공부노트 > 머신러닝, 딥러닝' 카테고리의 다른 글
| [코세라 강의 정리] 앤드류 응의 머신러닝 - Machine Learning System Design (0) | 2021.08.08 |
|---|---|
| [코세라 강의 정리] 앤드류 응의 머신러닝 - Advice for Applying Machine Learning (0) | 2021.08.07 |
| [코세라 강의 정리] 앤드류 응의 머신러닝 - Neural Networks (0) | 2021.08.01 |
| [코세라 강의 정리] 앤드류 응의 머신러닝 - Overfitting, Regularized (0) | 2021.07.31 |
| [코세라 강의 정리] 앤드류 응의 머신러닝 - Classification, Logistic Regression (2) (0) | 2021.07.31 |



